인공지능의 한계 2 - 변화하는 실세계를 해석하기 위한 데이터 사이언스

1. 서론

인공지능 역사에 있어서 슈퍼 인공지능(Artificial General Intelligence, AGI)에 대한 기대는 희망이 가득했으며 전문가들도 많이 언급해 왔습니다. 첫 황금기인 1950년 Marvin Minsky도 20년 내에 AI가 인간 수준에 도달할 것이라고 말을 했지만, 60년이 지난 지금도 슈퍼 AI는 나타나지 않았으며 몇십 년일지 몇백 년 후에나 가능할지 모릅니다. 딥러닝과 강화학습은 우리에게 무한한 지평을 암시하는 듯했지만, AI를 리드하는 딥마인드(DeepMind)도 5.7억 달러, 구글 스케일 하드웨어(고가 TPU), 3일간 1.2만 명의 연속학습(Continual Learning)에 준하는 엄청난 시간과 비용 대비 얼마나 큰 수익을 가져다주었는지에 대한 비판에 직면한 상태입니다. (19X19 바둑판 탐색 기술이 얼마나 큰 경제적 효과를 가져왔을까요?)

Gartner와 VentureBeat의 AI 리포트에 의하면, 80% 이상 AI/빅데이터 프로젝트가 실패로 끝났다고 합니다. Gartner의 Svetlana Sicular는 ‘2020년은 AI의 하강이 시작하는 해’라는 진단을 내놨고, 벤처캐피탈 펀드인 MMC Ventures는 유럽의 AI 스타트업을 조사한 뒤 이 중 40%가 아예 AI 기술을 쓰지 않는 것 같다고 발표했습니다. 역사상 등장한 1차, 2차 AI 겨울의 후속인 3차 겨울을 걱정하는 전문가들이 늘어나고 있지만, 그때와 달리 최근에는 가시화된 응용 상용화된 AI 사례들이 많아서 3차 겨울이 등장하지는 않을 것 같습니다.

최근 들어 AI의 거장 Yoshua Bengio, Yann LeCun, Geoffrey Hinton은 지금의 심층학습이 시스템 1인지 기술(예: 단순 지각)에 국한하는 것이며, 인간의 의식 흐름(Conscious Process)과 같은 것을 표현하는 시스템 2 인지 기술은 이제부터 시작해야 한다고 하면서 이를 DL 2.0이라 부르자고 합니다. 또한 Yann LeCun은 지속적인 단순 관측에 의해서 스스로 학습하는 자가지도학습(Self-Supervised Learning)을 AI의 미래라고 말하고 있습니다. 이제는 딥러닝의 잠재력을 전파하기보다는 한계를 인지하고 다시 도약할 미래의 방향을 찾아야 한다는 뜻입니다.

하지만 시스템 1인지 영역에 있어서 가장 강력한 심층학습 기술이 왜 수많은 응용 상용화로 직결되지 않는 이유는 무엇일까요? Gary Marcus (The Deepest Learning: Critical Appraisal)는 10가지 한계를 정리해서 발표를 했지만, 여기에서 응용 상용화 측면으로 좀 더 깊게 저수준의 한계들을 정리한다면 다음과 같은 기술적 이슈들로 정리 가능합니다.

   1. Unlabeled: 빅데이터(5천 개 이상) 이상의 인간의 레이블링 과정이 필수.
   2. Non-Independent Identically Distributed(IID): 훈련집합과 시험집합이 동일한 확률분포 구조가 아님.
   3. Adversarial Examples: 오염되는 관측 데이터.
   4. Miss-Labeled: 잘못된 학습집합 레이블.
   5. Class Imbalanced: 다양한 클래스들이 동등한 비율로 수집되지 않음.
   6. High-Dimensional Space: 원인인자와 무관한 비상관 고차원값들이 누적되어 왜곡된 수리통계적 거리로 계산.

우리가 많이 잘못 생각하는 것이 “강력한 계산 이론” 기반의 기계학습법이 없기 때문에 위에서 나열한 문제들이 해결되지 못하고 있다고 생각한다는 점입니다. 하지만, 원인은 실제 세계의 규칙성을 파악하기 위해 “레이블이 없는 조잡한" 데이터로부터 광범위한 신경망을 학습하는 견고한 기계학습 이론이 필요하다는 것입니다.

일례로 AI 기술이 도입되고 있는 판매량(수요) 예측은 삼성에서도 많은 연구와 투자를 하고 있는 영역임에도 불구하고 예측률이 높지 않기로 유명합니다. (수요예측 자체를 신뢰하지 않는 전문가들도 많습니다.) 이유는 판매량은 사람들의 감성을 비롯한 너무 많은 인자에 의해 영향을 받기 때문입니다. 이 중에서 극단적으로 틀린 수요예측 사례는 “갤럭시 노트 7의 배터리 폭파” 사고를 들 수 있습니다. 예측량과 (실제) 판매량의 차이는 당연히 클 수밖에 없었죠. 위에 언급한 6가지 문제 중 2번(독립항등분포)에 해당하는 사례입니다. 훈련세트에 갤럭시 배터리 문제가 정량화되어 있지 않았으므로, 판매량과의 원인 관계의 조건부 확률을 학습할 수 없었기 때문입니다.

일반적인 관점으로도 AI가 추론을 제대로 못 했을 것이라는 것에 누구나 다 동의하지만, 이 2번 “독립항등분포”의 조건이 데이터를 이용하여 학습하는 “귀납적 편향”을 가지는 (현) AI에 있어서 근본적인 한계임을 우리는 다시 한 번 검토해야 하고 이번 글에서는 이 한계에 대해서 논의하고자 합니다.

2. 통계적 기계학습에 “독립항등분포”가 왜 필요한가?

통계적 기계학습 용어는 매우 생소해 보이지만, 19세기 Legendre와 Gauss의 최소제곱법부터 시작하여 선형회귀, 로지스틱회귀, Breiman과 Friedman의 의사결정트리, 랜덤 포레스트에 이르기까지 현세대 머신러닝을 총칭할 정도입니다.

머신러닝이란 대상이 되는 자연현상을 관측에 의해서 표현한 데이터(훈련집합)를 이용하여 학습(예: 추정, 생성)하는 것이며, 모델의 성능을 표현하는 학습 오차를 계산하는 수단으로 확률분포를 이용한 통계적 거리가 사용됩니다.

여기에서 중요한 점은 관측 데이터의 훈련집합과 시험집합을 수집하는 과정에 있어서 약간의 가정과 제약을 둔다면, 낮은 훈련 오차를 가지는 모델은 시험집합에서도 매우 효과적이라는 점입니다. 약간의 가정이란 훈련집합과 시험집합 간에는 동일한 확률분포를 기반으로 하는 데이터 생성과정(Data Generation Process, DGP)을 거친다는 것과 두 집합의 각 샘플들은 서로 독립이라는 것입니다. 이 가정을 만족할 경우 사실상 두 집단의 차이는 인간이 붙인 이름뿐이며, 우리는 이 가정을 IID라고 부르고 IID 가정을 잘 따르는 학습 데이터를 이용한 통계적 기계학습 모델은 양 집합 전부 낮은 MSE(Mean Squared Error) 값을 가지게 되는 좋은 모델이라는 것입니다.

하지만 실제 자연현상의 거동을 관측하는 실제 학습 데이터가 동일한 데이터 생성과정을 가진다는 학습 이론을 잘 따를까요?

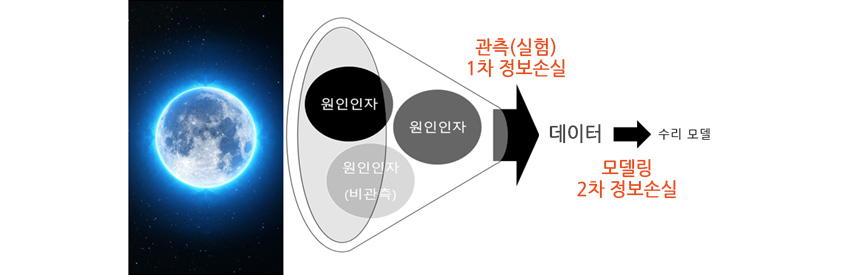
[그림 1] 1단계 정보손실, 2단계 정보손실 통계 모형

자연과학 측면에서는 어떤 현상을 관측하거나 실험으로 수집된 데이터에 인간의 해석을 부여하여 그 데이터에 숨어 있는 “자연의 규칙 또는 구조”라 불리는 지배방정식을 찾아왔습니다. 문제는 [그림 1]에서 보면, 관측(Observation)과 실험(Experiment)이라는 1차 과정은 자연현상을 표현하는데 굉장히 많은 정보를 잃게 됩니다. 사실상 자연이 가지고 있는 정보는 너무나도 복잡하지만 현세대 인류의 “관측기술로는 이를 정확히 전부 보는 것이 불가능”합니다. 관측한 데이터로 모델을 만드는 과정에서 2차 정보량의 손실이 발생하지만, 이 부분은 좀 더 복잡한 수학 모델로 어느 정도 보정이 가능합니다. 만능근사(Universal Approximation) 이론이라는 딥러닝이 대표적인 기술입니다.

문제는 1차 정보량 손실 과정에서 관측이 불가능하지만, 현상에 영향을 주는 비관측인자들도 제외된다는 것과 그나마 관측인자들마저 시간에 따라서 상태 전이가 발생한다는 것 때문에 시간이 지남에 따라 관측 데이터의 가치와 신뢰도도 급격히 떨어진다는 것입니다. 즉, 앞서 말한 “고정된 일부의 훈련집합”이라 불리는 샘플 데이터는 자연현상에 비하면 매우 “조잡한” 정보량을 가지고 있다는 것입니다. 현세대 AI를 이끌어온 주류 세력은 이 문제에 대해서 노골적으로 다루진 않았지만, 다른 후발 전문가(조우쯔화, 왕주에)들은 독립항등분포 가정이 머신러닝이 실세계를 표현하는 데 한계가 있음을 지적하고 있습니다.

3. 변화하는 실세계 공간은 “독립항등분포”를 따르는가?

이 한계는 최근에 논의된 것이 아닙니다. 통계 이론의 시작인 Pearson, Fisher, Neyman, Kolmogorov 세대부터 시작한 해결되지 않은 문제입니다. Kolmogorov의 확률에 대한 정의는 “발생할 수 있는 모든 사건들의 집합이고, 이 사건집합의 크기를 계산하여 확률 공간을 정량화할 수 있다”는 것입니다. 머신러닝에 사용하는 훈련/시험집합이 이 현실 세계의 사건 기반 데이터로 정량화한 것입니다.

그럼 사건들의 집합이란 현실 세계에서 무엇일까요? Gosset은 ‘실험에서 발생할 수 있는 모든 경우의 집합’이라고 정의했고, 교과서에서는 {우산, 비옷}을 사용한다는 사건은 {비, 눈}이 온다는 근원 사상에 대한 집합들로 계산한다고 설명합니다. 하지만 이것들은 매우 단순화한 이론적인 해석일 뿐입니다.

실험에 영향을 미치는 모든 사건의 공간이란 것은 현실에서 무엇이고 어디서부터 어디까지 계산해야 할까요? 누구나 다 동일하게 계산할 수 있는 사건의 정의 기준은 무엇일까요? 이 확률의 정의에 대해서는 통계학의 천재들도 직접적인 대답을 회피하였습니다. (길가에 보이는 구멍은 어떤 사건에 의해서 만들어질까요? 지나가던 우주인이 뚫었을 확률은?)

현대 통계학의 아버지인 Fisher(1890년 출생)는 확률 공간을 다음과 같이 정의하여 자연현상을 분석했습니다. “실험 계획에 의해서 관측된 데이터(임의 샘플링)들만이 전체(모집단)를 대변하는 부분집합이기 때문에 도출된 통계적 유의성(p-value)은 자연현상의 인과관계를 설명할 수 있다.” 확실히 Fisher의 확률공간에 대한 수리 모델은 현실 실세계를 부분적으로 잘 반영하였습니다. 하지만 여기서 너무나 어려운 조건이 숨어 있습니다. 우리가 “실험 계획에 의한 표본공간으로 자연현상을 모두 데이터화”할 수 있다면 말이죠.

Fisher 역시 수십 년간 실험 데이터를 분석한 결과, 밀 수확량이 강수량과 비료성분 비율에만 영향을 받지 않고, 알 수 없는 비관측 인자들에 의한 효과가 존재하며 토지 비옥토 자체도 시계열 변화가 있음을 깨달았습니다. 관측치 간에 독립이 아닌 시간의 흐름에 따른 상관성을 갖는 문제가 있다는 것이며, 앞서 말한 독립항등분포의 독립성을 위반한다는 것이죠. 이는 Box와 Kolmogorov의 확률적 과정(Stochastic Process)으로 어느 정도는 해결을 할 수 있는 것처럼 보였지만, 비관측 인자에 의한 밀 수확량의 변동 문제는 자신의 통계기법으로는 한계가 있다는 것을 Fisher는 말년에 깨달았습니다.

다른 사례로는 우리가 잘 아는 동전던지기가 있습니다. 무한에 가까운 실험을 하더라도 앞에 던진 동전이 ‘앞면’이 나왔다 하더라도 다음 던진 동전이 ‘앞’, ‘뒤’일 확률에는 영향을 주지 않는다는 것이죠. 이는 확률 시스템계를 매우 한정된 공간으로 볼 경우에만 가능한 논리입니다. 실제로는 동전을 무한히 던지는 순간 동전이나 실험기기에 마모가 발생하거나 손가락이 피로해져서 ‘앞’, ’뒤’ 확률에 영향을 주기 시작하는 경우가 발생한다는 것입니다. 즉, 확률 시스템계에서 벗어나 관측되지 않는 마찰(Friction)이라는 비관측인자가 마모라는 효과를 발생시키면서 우리가 배운 50% 확률을 위반하는 경우를 만들게 되는 것입니다.

그럼 실세계에서 독립항등분포가 잘 맞는 경우는 없는 것일까요? 많은 외란들(비관측인자이자 불확실성 요소)이 잘 통제된 인공적인 공간인 시뮬레이션, 게임, 실험실에서는 이런 IID 조건도 그리고 유명한 마코브 프로세스(Markov Process)도 잘 들어맞습니다. 다만 인간이 인위적으로 만든 세계(시뮬레이션) 외에는 독립항등분포를 보기가 쉽지 않다는 것이 문제인 것입니다. Gauss가 말하던 흔히 보는 분포라는 의미의 “Normal Distribution”이 얼마나 우리 주변에서 볼 수 있을까요? 오히려 특정 분포 중의 하나라는 말이 더 적합할 수 있습니다.

4. 변화하는 실세계를 어느 정도 학습이 가능한가?

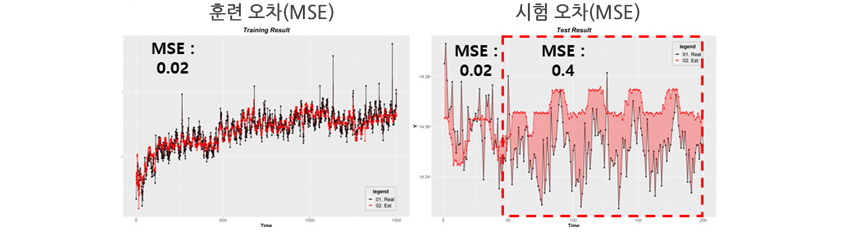
[그림 2] 화학물질 도포 예측

제조공정에 있어서 어떤 성분과 공정 조건에 따라서 화학물질을 배합하며 대상 표면에 화학물질을 균질하게 도포가 가능한지 예측하는 문제가 있었습니다. [그림 2]에서 왼편의 검은색 포인트(라인)들은 도포된 표면(Y)의 두께를 실제 관측한 결과이며, 붉은색 포인트(라인)들은 일반적인 예측 모델(배치학습) 결과입니다. 훈련 오차(MSE)가 낮아 좋은 예측 모델이라고 생각할 수 있습니다.

당연히 훈련집합의 오차가 낮으니 IID가정에 의해서 시험집합에서도 낮은 오차가 나올 것이라 예상했습니다. 하지만 [그림 2]의 오른편을 보면 실제 시험 오차는 처음에 훈련 오차와 비슷해 보이지만, 점차 시간이 지날수록 오차가 커지는 것을 볼 수가 있습니다. 관측인자들의 내부 화학 물성치가 변화하지만, 학습 모델의 계수들이 이를 반영하지 못한 문제입니다. 흔히 실험실에서 높은 성능을 보이는 학습 모델이 실제 테스트 환경에서 낮은 성능을 보이는 사례 중 한 가지입니다.

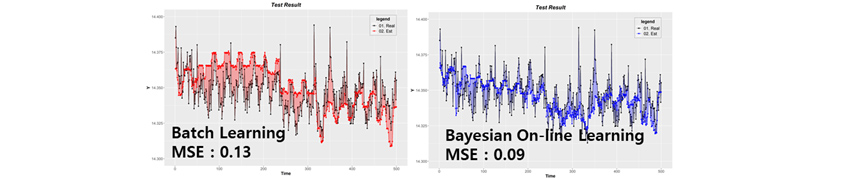
이런 경우는 다행히 관측인자들의 내재적 물성치 변화에 의해서 데이터 드리프트가 발생하는 것이기 때문에, 베이지안 기반 재학습 기술로 이를 어느 정도 해결할 수가 있습니다. [그림 3]에서 일반 배치학습법 기반 예측 모델 대비 베이지안 기반 온라인 예측 모델이 개선된 효과를 보이는 것을 확인할 수 있습니다.

[그림 3] 배치학습법 예측 모델 vs. 베이지안 예측 모델

이런 경우 고정된 학습집합 전부를 한 번에 학습하는 배치학습법이 아닌, 관측 상태에 따라 스스로 모델을 능동적으로 변경하는 능동적 미니배치 학습 계열이 더 효과적일 수 있다는 것입니다. 이런 식으로 경험한 자료 집합을 한 번만 학습하는 방식이 아닌, 또 다른 학습 이론을 필요로 합니다. 물론 또 다른 학습 방법으로는 강화학습과 같은 기법을 생각해 볼 수 있습니다. 하지만 강화학습은 상태 전이 확률을 마르코프 프로세스와 몬테카를로(Monte Carlo)를 이용하여 무작위로 수많은 시행착오를 통해서 학습하는 방식으로 데이터 수집 시간이 오래 걸리며, 그나마 학습한 상태 전이 확률이 달라지는 문제에 대해서는 직접적인 해결책이 아닙니다.

5. 결론

우리가 사용하는 학습 데이터는 자연계 일부 정보량만 포함한 샘플일 뿐입니다. 가장 높은 성능을 보이는 딥러닝도 주어진 수많은 잘 정제된 이미지들의 픽셀 간 비선형 공간 상관성을 잘 표현하는 정교한 통계 모델일 뿐이지 조잡하게 관측된 데이터로 실세계 자연현상을 정확히 학습하는 만능의 기술이 절대 아닙니다. 따라서 편향된 데이터 샘플로 컴퓨터가 ‘경험’하여 학습한 수준은 고대부터 인류의 ‘경험’에 의해서 찾아낸 지배방정식과는 아직까지도 큰 차이가 있습니다. 관측된 데이터를 통해서 얻은 수리 모델은 자연현상의 일부만 해석하거나 틀리게 해석하는 일이 너무나 당연합니다. 이렇듯 자연현상의 “데이터 생성과정”과 “수리통계적 확률과정”은 동치를 이루지 않는다는 것이 우리 데이터 분석가들이 직면하고 있는 현실인 것입니다.

통계학의 천재들도 실제 확률에 대한 대답은 회피하였듯이, 현실 세계의 인과관계를 가지는 모든 사건을 정확하게 보는 것 자체가 아직은 불가능합니다. 우리는 부정확하고 조잡한 정보를 기반으로 수리모델을 만들어야 함을 인정하고 그 모델은 현실을 왜곡한 불확실성으로 가득하다는 것을 알아야 합니다. 실세계에서 확률의 정의를 찾아내려는 노력은 Fisher, Neyman, Kolmogorov 이후로 어느 누구도 이어받지 못한 채 남아 있으며 이를 해결할 천재는 아직 나타나지 않고 있습니다.



References
[1] “THE LADY TASTING TEA: HOW STATISTICS REVOLUTION IN THE 20TH CENTURY”, DAVID SALSBURG
[2] “FROM SYSTEM 1 DEEP LEARNING TO SYSTEM 2 DEEP LEARNING.”, YOSHUA BENGIO, NEURIPS 2019



▶  해당 콘텐츠는 저작권법에 의하여 보호받는 저작물로 기고자에게 저작권이 있습니다.
▶  해당 콘텐츠는 사전 동의 없이 2차 가공 및 영리적인 이용을 금하고 있습니다.