
들어가며
지난 1편 ‘양자컴퓨팅으로 더 커지는 보안 위협, 지금이 바로 PQC 전환을 시작할 때!’에서는 다가오는 양자컴퓨팅 시대에 암호화 기술에 대한 보안 위협과 이를 대비하기 위한 PQC 알고리즘 표준화 현황에 대해 간략히 소개하였습니다. 이와 더불어 현재 IT 시스템에 적용된 기존 암호화 기술을 양자내성암호로 전환하는 PQC Migration을 왜 지금부터 준비해야 하는지도 함께 알아보았는데요, 이번 편에서는 인터넷 보안의 기반이 되는 암호화 기술과 이를 공격하는 양자 알고리즘의 원리에 대해 알아보고, 이에 대비하는 PQC 알고리즘 표준화 현황에 대해 살펴보겠습니다.
스마트폰이 없는 하루를 상상해 보신 적이 있나요? 우리는 하루에도 수십번씩 스마트폰을 통해 다양한 인터넷 기반 서비스 이용하고 있습니다. 모바일 메신저, SNS, 클라우스 서비스 등을 이용해 개인적인 사진이나 메시지를 주고받기도 하고, 인터넷 쇼핑, 모바일 뱅킹, 암호 화폐 거래 등을 통해 금융 관련 데이터를 주고받기도 합니다. 최근에는 병원 예약이나 건강검진 결과 확인 등 의료 관련 정보까지도 인터넷 기반 서비스를 이용하여 데이터를 주고받고 있는데요, 이러한 데이터들은 어떻게 보호되고 있을까요?
새로운 모바일 앱을 설치하거나 인터넷을 통해 새로운 서비스에 회원 가입할 때 자주 보는 문구가 있습니다. '고객의 데이터는 암호화를 통해 안전하게 보호됩니다'라는 메시지를 한 번쯤 읽어본 기억이 있으실 텐데요, 암호화는 어떤 기술일까요? 여기서 말하는 암호화 기술은 서비스 로그인 시 사용자 아이디와 함께 입력하는 패스워드와 구분되는 개념으로, 원본 메시지를 쉽게 알아볼 수 없도록 임의의 메시지로 변환하는 기술을 말합니다. 구체적으로는 원본 메시지를 임의의 메시지로 변화하는 과정을 ‘암호화(Encryption)’ 과정이라 하고 이 임의의 메시지를 ‘암호문’이라고 합니다. 암호문을 다시 원본 메시지로 복원하는 과정을 ‘복호화(Decryption)’ 과정이라고 하는데요, 암/복호화 과정에서는 각각 ‘암호화키(Encryption Key)’, ‘복호화키(Decryption Key)’를 이용해 원본 메시지를 암호문으로 변환하거나 암호문을 다시 원본 메시지로 복원합니다. 이러한 암호화 기술은 크게 두 가지로, 암호화키와 복호화키가 같은 ‘대칭키 암호화 기술’과 암호화키와 복호화키가 서로 다른 ‘비대칭키 암호화 기술’로 분류됩니다. 대칭키 암호화 기술(이하 "대칭키 암호"라 합니다)에서는 서로 같은 키를 이용해 암/복호화하기 때문에, 사전에 암/복호화 당사자 간 키 합의 과정이 필요하며 다른 사용자에게 노출되지 않도록 안전하게 관리해야 합니다. 대칭키 암호화와 달리 비대칭키 암호화 기술에서는 암호화키를 공개하여 누구나 메시지를 암호화할 수 있도록 하고 정당한 복호화키 소유자만이 암호문을 복호화할 수 있도록 보장합니다. 이와 같이 누구나 암호화할 수 있도록 암호화키를 공개하는 특징을 들어 비대칭키 암호화 기술을 ‘공개키 암호 기술’(이하 "공개키 암호"라 합니다)이라고도 합니다. 대칭키 암호는 암/복호화 처리 속도가 빠르며 암호문의 크기가 작은 특징이 있어 주로 대량의 데이터를 암호화하여 저장하는 용도로 사용합니다. 공개키 암호 역시 암/복호화 처리 속도가 빠르긴 하나 일반적으로 대칭키 암호에 비해 암/복호화 처리 시간이 더 걸리기 때문에 데이터 암호화 목적으로 사용하기보다는 대칭키 암호에 사용되는 암/복호화키 합의에 주로 사용합니다. 공개키 암호의 또 다른 사용 예로는 전자서명 기술을 이용한 공동인증서 등이 있습니다.
우리가 매일 사용하는 모바일 메신저, 인터넷 쇼핑, 모바일 뱅킹 등 다양한 서비스의 보안은 대칭키 암호와 공개키 암호 기술을 기반으로 시작되는데요, 양자컴퓨터가 개발되면 인터넷 보안의 기반이 되는 암호화 기술의 안전성을 더 이상 보장할 수 없게 됩니다. 다음 장에서는 대칭키 암호와 공개키 암호에 대한 양자 공격 알고리즘에 대해 좀 더 알아보겠습니다.
양자 공격 알고리즘의 원리
암호화 기술에 대한 보안 위협은 양자 공격 알고리즘이 개발되며 시작되었는데요, 대표적인 양자 공격 알고리즘으로는 Grover 알고리즘과 Shor 알고리즘이 있습니다. 이들 알고리즘의 원리를 살펴보기에 앞서 양자컴퓨터와 관련된 몇 가지 기본 개념에 대해 먼저 알아보겠습니다. 양자컴퓨터(Quantum Computer)란 기존 디지털 컴퓨터와 구분되는 개념으로, 미국의 물리학자 리처드 파인만 등에 의해 고안되었습니다. 양자컴퓨터는 양자 역학의 법칙에 기반하여 양자 얽힘(Quantum Entanglement), 중첩(Superposition) 등의 효과를 이용해 계산을 수행하는 컴퓨터를 말합니다. 본 기고문에서는 Grover 알고리즘과 Shor 알고리즘의 원리를 이해를 돕는 목적으로 '양자 상태(Quantum State)'와 '측정(Measurement)', '확률 진폭(Probability Amplitude)', '양자 중첩(Quantum Superposition)'의 핵심 아이디어만을 예로 들어 소개하겠습니다.
0과 1의 비트 연산(Bitwise Operation)에 기반하는 기존 디지털 컴퓨터와 달리 양자컴퓨터는 0과 1의 비트뿐만 아니라 0과 1이 동시에 공존하는 상태도 함께 계산에 활용합니다. 여기서 0과 1이 동시에 공존하는 상태는 무엇을 의미할까요? 이를 설명하기에 앞서 기존 컴퓨터의 동작 원리부터 살펴보겠습니다. 현재 우리가 사용하는 디지털 컴퓨터에서는 0 또는 1의 한 가지 상태로 결정된 비트들을 이용해 정수의 덧셈, 뺄셈과 같은 간단한 연산부터 공개키 암호의 암/복호화 연산 등 복잡한 연산까지 수행합니다. 0 또는 1 중 한 가지로 결정된 상태는 마치 우리 손바닥 위에 놓인 하나의 동전과 같이 생각할 수 있는데요, 일반적인 동전이라면 앞면 또는 뒷면 중 한 면을 위로하고 손바닥 위에 놓여있을 것입니다. 이와 달리 0과 1이 공존하는 상태는 동전을 공중으로 던진 후 손바닥에 올려놓기 전까지의 장면을 상상하면 이해하기 쉽습니다. 공중에서 계속 회전하고 있는 동전 역시 우리가 손바닥에 올려놓는 순간 앞면 또는 뒷면의 한 가지 상태로 결정이 되겠지만 손바닥에 올려놓기 전까지는 앞면이 나올지 뒷면이 나올지 확실하지 않습니다. 다만 우리는 50% 확률로 앞면이, 나머지 50% 확률로 뒷면이 나올 거라고 예상할 뿐이죠. 이와 같이 공중에서 회전 중인 상태를 0과 1이 공존하는 '양자 상태'라고 이해할 수 있고, 손바닥에 올려놓아 앞면 또는 뒷면을 결정하는 행위는 양자 상태를 '측정'하는 것으로 이해할 수 있습니다. '확률 진폭'은 앞면과 뒷면이 나올 확률을 결정하는 값으로 이해할 수 있고, '확률 진폭'의 크기에 따라 앞면과 뒷면이 나올 확률이 커지거나 작아질 수 있습니다. (여기서도 전체 확률의 합은 언제나 100%로 앞면이 나올 확률이 커지면 뒷면에 나올 확률을 작아집니다). '양자 중첩'은 앞면과 뒷면이 공존하는 '양자 상태'를 각각의 '확률 진폭'을 고려하여 더해진 상태를 표현한 것으로 이해할 수 있습니다.
양자컴퓨터와 기존 디지털 컴퓨터를 비교해 다시 한번 정리하면, 기존 컴퓨터는 손바닥 위에 놓인, 앞면 또는 뒷면으로 결정되는 동전들을 이용해 연산을 수행하는 것과 같고, 양자컴퓨터는 공중에서 회전하고 있는 동전의 '양자 상태'까지 함께 고려해 연산을 수행하는 것과 같습니다. 여기서 중요한 점은 양자컴퓨터에서는 '측정'이 되기 전의 '양자 중첩' 상태를 조종하여 '확률 진폭'을 변화시킬 수 있으며, 이를 통해 특정값이 '측정'될 확률을 높일 수 있다는 점입니다.
대칭키 암호를 위협하는 Grover 알고리즘
Grover 알고리즘은 1996년 인도의 컴퓨터 과학자 Lov Grover에 의해 고안된 양자 알고리즘으로, 정렬되지 않은 수많은 데이터의 집합에서 특정 조건을 만족하는 단 하나의 값을 찾아주는 알고리즘입니다. 데이터 집합이 정렬되어 있지 않기 때문에 기존 컴퓨터에서 우리가 찾고 싶은 '그 값'을 찾기 위해 운이 나쁜 경우 전체 데이터를 모두 한 번씩 확인해야 할 수도 있는데요, Grover 알고리즘에서는 양자 중첩을 활용하여 문제를 좀 더 빠르게 해결합니다. 개념적으로 Grover 알고리즘은 전체 데이터가 중첩된 양자 상태를 준비하고, 우리가 찾고 싶은 '그 값'이 측정될 확률이 높아지도록 양자 상태를 조종하여 확률 진폭을 변화시킨다는 아이디어입니다.
기본적으로 대칭키 암호의 안전성은 암/복호화키의 비밀성에 의해 보장됩니다. 이를 위해 암/복호화키는 충분히 큰 집합(이하 "키 공간"이라 합니다)에 포함된 임의의 값임이 보장되어야 합니다. 암/복호화 당사자가 사용하는 특정 암/복호화키는 키 공간에 포함된 수많은 값 중 하나의 값으로, 해당 키로 암호화된 암호문을 유효하게 복호화할 수 있는 단 하나의 값을 의미합니다. 여기서 Grover 알고리즘을 이용하면 "암호문을 유효하게 복호화할 수 있다"는 특정 조건을 만족하는 단 하나의 값, 즉 암/복호화키를 좀 더 빠르게 찾을 수 있습니다. 즉, Grover 알고리즘으로 인해 대칭키 암호의 안전성이 훼손되어, 이를 대비하기 위해서는 더 큰 키 공간을 사용해야 한다는 의미입니다. 예를 들어, 데이터 암호화를 위해 국제 표준 대칭키 암호인 AES-128(키 길이: 128-bit)을 사용하고 있었다면, 좀 더 큰 키 공간을 가지도록 AES-256(키 길이: 256-bit) 또는 AES-512(키 길이: 512-bit)로 변경해야 합니다.
공개 키 암호를 위협하는 Shor 알고리즘
공개키 암호의 안전성은 공개된 암호화키(이하 "공개키"라 합니다)나 암호문으로부터 복호화키(이하 "비밀키"라 합니다) 또는 원본 메시지를 복원하기 어려운 정도만큼 보장됩니다. 이를 위해 공개키와 비밀키 간에는 긴밀한 수학적 관계가 성립하는 동시에, 공개된 정보로부터 비밀 정보를 계산하는 문제가 수학적으로 충분히 어렵다(문제를 푸는 데 충분히 긴 시간이 걸린다)는 점이 보장되어야 합니다. 예를 들어, 대표적인 공개키 암호인 RSA 암호에서는 임의의, 충분히 큰 임의의 두 소수(Prime Number) p, q를 골라 비밀키로 하고 두 수의 곱 N=p*q를 공개키로 합니다. 여기서 공개키 N과 비밀키 p, q 간에는 N=p*q라는 수학적 관계가 성립하는 동시에, 공개키 N으로부터 비밀키 p, q를 찾는 소인수분해 문제의 수학적 어려움이 알려져 있습니다. 또 다른 예로, 타원곡선 기반 암호의 안전성은 수학적으로 어려운 문제라고 알려진 이산대수 문제에 기반하고 있습니다. 그러나 불행히도, 이 문제들의 어려움은 기존 컴퓨터에서만 보장할 수 있으며, 양자컴퓨터가 개발되면 Shor 알고리즘에 의해 소인수분해 문제와 이산대수 문제의 어려움을 보장할 수 없습니다.
Shor 알고리즘은 1994년 미국의 수학자 Peter Shor에 의해 고안된 양자 알고리즘으로, 이 알고리즘을 이용하면 소인수분해 문제와 이산대수 문제를 충분히 빠르게 해결할 수 있습니다. Shor 알고리즘이 해결하는 문제는 ‘숨겨진 부분군 문제(Hidden Subgroup Problem)’라고 하는데요, 이 문제를 RSA 암호를 예로 생각해 볼까요? RSA 암호의 공개키 N과 비밀키 P, q에 대하여, 숨겨진 부분군 문제는 a^r-1이 N으로 나누어 떨어지는 두 정수 a와 r을 찾는 문제입니다. 이러한 문맥에서, Shor 알고리즘은 주어진 N에 대하여 위 조건을 만족하는 (a, r) 쌍을 확률적으로 찾아주는 양자 알고리즘입니다. 여기서 중요한 점은 적절한 (a, r)을 한 쌍이라도 찾을 수 있다면 RSA 암호의 안전성이 완전히 훼손된다는 점입니다. 예를 들어, a와 r이 모두 1과 N이 아니며, r=2k가 짝수인 (a, r)을 한 쌍이라도 찾았다면, 두 정수 a^k-1과 N의 최대공약수 또는 a^k+1과 N의 최대공약수를 계산함으로써, 비밀키 p와 q를 얻을 수 있습니다. 최대공약수를 계산하는 문제는 기존 컴퓨터에서도 아주 빠른 시간 안에 풀 수 있는 문제이기 때문에 양자컴퓨터가 개발되면 Shor 알고리즘을 이용해 RSA 암호를 무력화할 수 있습니다. Grover 알고리즘과 비슷하게 Shor 알고리즘 역시 개념적으로는, 수많은 (a, r) 쌍의 후보들이 중첩된 양자 상태를 준비하고, N의 소인수 찾기에 힌트가 되는 적절한 (a, r) 쌍이 측정될 확률이 높아지도록 양자 상태를 조종하여 확률 진폭을 변화시킨다는 아이디어입니다. 다음 장에서는 공개키 암호가 무력화되면 발생할 수 있는 문제와 Shor 알고리즘이라는 보안 위협에 대비하기 위한 양자내성암호에 대해 알아보겠습니다.
양자내성암호, PQC 알고리즘
지금까지 현재 사용되는 암호화 기술에 대한 두 가지 양자 공격 알고리즘에 대해 알아보았습니다. 첫 번째로는 대칭키 암호의 안전성을 훼손하는 Grover 알고리즘으로, 이를 대비하기 위해서는 기존보다 더 큰 키 길이를 사용할 것을 권장합니다. 두 번째로는 공개키 암호를 무력화하는 Shor 알고리즘으로, 이를 대비하기 위해서는 소인수분해 문제 또는 이산대수 문제와 전혀 다른 수학적으로 어려운 문제에 기반하는 새로운 공개키 암호가 필요합니다 [표 1]. 특히, Grover 알고리즘, Shor 알고리즘 외에도 양자 공격 알고리즘이 알려지지 않은 새로운 수학 문제에 기반한 공개키 암호가 필요한데요, 이들 암호화 기술을 통틀어 양자내성암호(Post Quantum Cryptography - 이하 "PQC"라 합니다)라고 합니다. 현재까지 제안된 PQC 알고리즘으로는 암호격자 기반 암호(Lattice-based Cryptography), 코드 기반 암호(Code-based Cryptography), 다변수다항식 기반 암호(Multivariate Polynomial Cryptography), 해시 기반 전자서명(Hash-based Signature) 등이 있습니다. PQC 알고리즘 표준화 현황에 대해서는 뒤에서 계속 알아보도록 하고, 그 전에 현재 사용되는 RSA 암호화 또는 타원곡선 기반 암호가 무력화되면 어떤 문제가 발생할지 살펴보겠습니다.
| 암호화 알고리즘 | 구분 | 사용 목적 | 양자컴퓨팅 보안 위협 현황 |
|---|---|---|---|
| AES | 대칭키 암호 | 데이터 암호화 | 더 큰 키 길이 필요 |
| SHA-2, SHA-3 | - | 해시 함수 | 더 큰 출력값 필요 |
| RSA | 공개키 암호 | 전자서명, 암/복호화 키 합의 | 안전하지 않음 |
| ECDSA, ECDH | 공개키 암호 | 전자서명, 암/복호화 키 교환 | 안전하지 않음 |
| DSA | 공개키 암호 | 전자서명, 암/복호화 키 교환 | 안전하지 않음 |
인터넷 통신을 보호하기 위해 사용되는 TLS 암호 프로토콜에서는 공개키 암호를 통해 서버와 클라이언트 간 암호화 통신에 사용할 암/복호화키를 설정합니다. 모바일 뱅킹 앱을 사용하거나 인터넷을 통한 암호화폐 거래 시에는 공개키 암호를 통해 정당한 사용자임을 증명하여 금융 거래를 안전하게 보호합니다. 그런데 양자 공격 알고리즘에 의해 현재 사용되는 공개키 암호가 무력화된다면 모바일 메신저를 통해 주고받는 텍스트 메시지, 사진, 동영상 등이 모두 유출되거나, 나도 모르는 사이 내 계좌에 보관된 돈이 다른 사람의 계좌로 보내질 수도 있습니다.
이 모든 문제들은 ‘Grover 알고리즘과 Shor 알고리즘을 실제로 수행할 수 있는 양자컴퓨터가 개발된다’는 가정에서 시작되는데요, 많은 전문가들이 향후 10년 이내에 현재 인터넷 보안의 근본을 무너뜨릴 만큼 강력한 양자컴퓨터(Cryptographically Relevant Quantum Computers - 이하 "CRQC"라 합니다) 개발이 이뤄지기는 어려울 것으로 전망하고 있습니다. 그러나 아직 안심하긴 이릅니다. CRQC가 개발되지 않더라도, Harvest Now Decrypt Later(이하 "HNDL"라 합니다) 공격은 현재도 유효하기 때문입니다. HNDL 공격에 대비하기 위한 PQC 하이브리드 키 설정 방법은 현재도 적용 가능합니다. HNDL 공격에 대한 자세한 설명은 지난 기고문을 참고하시기 바랍니다.
PQC 알고리즘 표준화를 위해 미국 국립표준기술연구소(National Institute of Standards and Technology, NIST)에서는 2017년부터 표준 알고리즘 공모를 진행 중이며, 2023년까지 초안 표준 완료를 목표로 하고 있습니다. 현재까지 키 교환 알고리즘(Key Encapsulation Mechanism, KEM) 1종과 전자서명 알고리즘(Digital Signature) 5종을 표준 알고리즘으로 선정하였고 [표 2], 추가로 키 교환 알고리즘 3종을 평가 중에 있으며 전자서명 표준 알고리즘에 대한 추가 공모도 함께 진행하고 있습니다. 국내에서는 한국 양자내성암호연구단에서 PQC 알고리즘 표준화를 진행하고 있습니다. 이처럼 우리나라뿐만 아니라 미국, 유럽, 일본, 중국에서도 PQC 알고리즘 표준화와 함께 PQC 알고리즘으로의 전환(이하 "PQC Migration"이라 합니다)을 준비하고 있습니다.
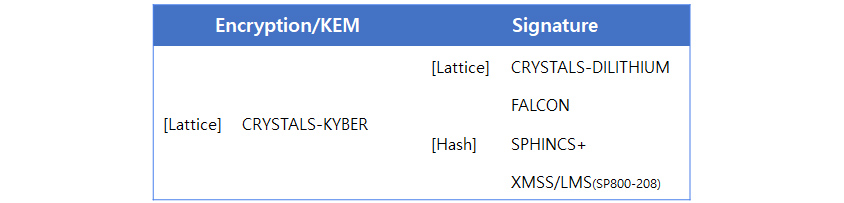
- [lattice] CRYSTALS-KYBER
- [lattice] CRYSTALS-DILITHIUM , FALCON
- [hash] SPHINCS+ , XMSS/LMS
마무리하며
지금까지 암호화 기술에 대한 보안 위협과 이를 대비하기 위한 방법을 알아보았습니다. 특히, 현재 사용되는 공개키 암호의 경우 Shor 알고리즘을 통해 무력화되므로 PQC 알고리즘으로의 전환이 필수적이라고 설명하였습니다. 즉, 양자컴퓨터로 인한 보안 위협에 대비하기 위해 현재 RSA 암호나 타원곡선 기반 암호가 적용된 곳을 모두 찾아 PQC 표준 알고리즘을 적용하는 PQC Migration을 시작해야 합니다.
PQC Migration이라는 정답이 나와있는 상태지만 아직 해결해야 할 문제는 많이 남아있습니다. 일반적으로 PQC 알고리즘은 기존 RSA 암호나 타원곡선 기반 암호에 비해 키와 암호문이 커지기 때문에 PQC 알고리즘을 적용할 수 있도록 전체 시스템의 개편이 불가피합니다. 또한, 기존 공개키 암호 사용 현황을 파악하기 위해 전체 암호화 기술 사용 현황을 포함한 전체 인프라에 대한 인벤토리를 작성해야 합니다. 작성된 인벤토리와 함께 해당 암호화 기술이 보호하는 대상 데이터의 중요도, 유출 시 발생하는 위험 비용 및 관련 규제 등을 고려하여 PQC 알고리즘 적용이 시급한 정도에 따라 순차적으로 PQC Migration을 진행해야 할 것입니다.
이처럼, 효과적인 PQC Migration을 위해서는 양자 공격에 취약한 암호 사용 인벤토리 확보와 기존 리스크 관리 시스템을 확장하는 양자 컴퓨팅 관련 리스크를 복합적으로 관리하는 리스크 관리 시스템과 리스크 평가 프레임워크가 필요합니다. 3편에서는 양자 컴퓨터 관련 리스크 관리 방법과 함께 암호 민첩성(Crypto Agility) 개념에 대해 알아보고, PQC Migration 전략에 대해 살펴보도록 하겠습니다.
References
[1] https://scottaaronson.blog/?p=208
[2] https://nvlpubs.nist.gov/nistpubs/ir/2016/NIST.IR.8105.pdf
[3] Quantum Computing Risks to the Financial Services Industry, ASC X9 IR-F01-2022(2022.11.29 공개)
https://x9.org/wp-content/uploads/2022/11/X9F-Quantum-Computing-Risk-Study-Group-IR-F01-2022_20221129-Published-PDF.pdf
▶ 해당 콘텐츠는 저작권법에 의하여 보호받는 저작물로 기고자에게 저작권이 있습니다.
▶ 해당 콘텐츠는 사전 동의 없이 2차 가공 및 영리적인 이용을 금하고 있습니다.
![]()

조지훈 | 삼성SDS 연구소 보안연구팀장
삼성SDS 연구소 보안연구팀장으로 양자내성암호와 같은 암호기술, 개인정보보호 강화 기술, 그리고 클라우드 보안 기술을 연구개발하고 있습니다.
윤효진 | 삼성SDS 연구소 보안알고리즘Lab장
암호학을 전공하였으며, 삼성SDS 연구소 보안알고리즘Lab장으로 양자내성암호 원천 기술 및 전환 기술, 개인정보보호 강화 기술을 연구개발하고 있습니다.
김은경 | 삼성SDS 연구소 보안알고리즘Lab
타원곡선암호 등 현대암호학의 기반이 되는 수학 이론을 전공하여 박사학위를 취득하였습니다. IT 시스템 곳곳에 적용된 암호기술을 식별하여 안전하고 효율적으로 양자내성암호를 적용하기 위한 양자내성암호 전환 기술을 연구개발하고 있습니다.
