AI 기반 물리 정보 신경망을 이용한 시뮬레이션

2023-01-18 문기효

이번 글에서는 시뮬레이션에서 최근 화두가 되고 있는 물리 정보 신경망(Physics-Informed Neural Network, 이하 PINN)에 대해서 다루어 보겠습니다. 여기서 시뮬레이션이라는 것은 유체역학, 전자기학 등 공학 문제를 슈퍼컴퓨터를 이용한 수학적인 방법으로 푸는 것을 말합니다. 자동차 형상, 휴대폰 열설계, 반도체 소자 시뮬레이션 등이 있습니다.

전통적으로 시뮬레이션은 유한차분법(Finite Difference Method), 유한요소법(Finite Element Method), 그리고 유한체적법(Finite Volume Method)이라고 하는 전체 도메인을 작은 요소로 나누어 근사적인 해를 구하는 수치해석적인 방법을 사용하여 시뮬레이션을 하였으며 이 과정에서 엄청난 양의 계산을 위해 슈퍼컴퓨터를 사용하였습니다.

하지만 최근 AI의 발전으로 인해 시뮬레이션 분야에도 AI를 접목시킨 물리 정보 신경망이라는 방법이 연구되기 시작하였습니다. 이 방법은 Inverse 문제와 Ill-posed 문제 등 전통적인 수치해석 기법의 한계를 극복하기 위해 대두되었습니다.

전통적인 수치해석 방법

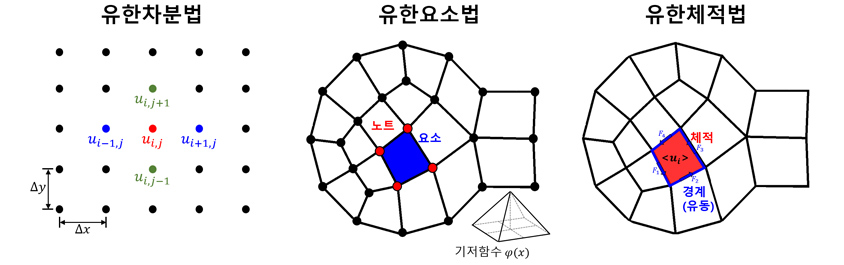
통상적으로 전통적인 수치해석 방법이라 함은 유한차분법, 유한요소법, 그리고 유한체적법이라고 할 수 있습니다. 이 세 가지 방법은 모두 도메인을 잘게 요소(Element)로 나누어 각 요소에서 수치해석적인 방법을 적용하여 계산합니다. 이렇게 각 요소에서 계산한 값을 모아서 시뮬레이션을 수행합니다.

[그림 1] 유한차분법, 유한요소법, 유한체적법의 차이

유한차분법의 경우 함숫값의 차이를 이용한 미분계수를 근사하여 편미분 방정식을 푸는 방법입니다. 전방(forward), 후방(backward), 중앙(central) 차분법 등 세 가지로 나눌 수 있으며 테일러 급수 전개를 통해 유도합니다. 직사각격자에 적합하고 알고리즘이 직관적이어서 사용하기 쉽고 병렬계산에 적합하여 학술적인 연구나 간단한 시뮬레이션을 할 경우에 효과적입니다. 선형 문제뿐만 아니라 비선형 문제에도 쉽게 적용 가능하며 특히 유체역학 시뮬레이션에 많이 사용됩니다.

유한요소법의 경우 풀고자 하는 편미분방정식을 적분형으로 표현한 뒤 최종적으로 Ax=b 형태의 선형시스템으로 변환하여 근사해를 구하는 방법입니다. 주로 고체역학이나 전자기학 시뮬레이션 등에 사용되며 GPU 가속 효과가 가장 크고 불규칙한 물체 시뮬레이션에 적합합니다. 유한차분법에 비해 해의 연속성을 유지할 수 있기 때문에 물리적으로 타당한 해를 얻을 가능성이 높습니다.

유한체적법의 경우 보존 법칙을 만족하는 문제를 푸는데 적합하기 때문에 주로 유체역학 시뮬레이션에 사용됩니다. 유한체적의 면을 지나는 유동의 양을 기준으로 유도되며 시뮬레이션 형상에 대해 유연하게 계산을 적용할 수 있습니다. 유한차분법과 마찬가지로 불규칙한 물체를 시뮬레이션하는 데 적합합니다.

물리 정보 신경망의 특징

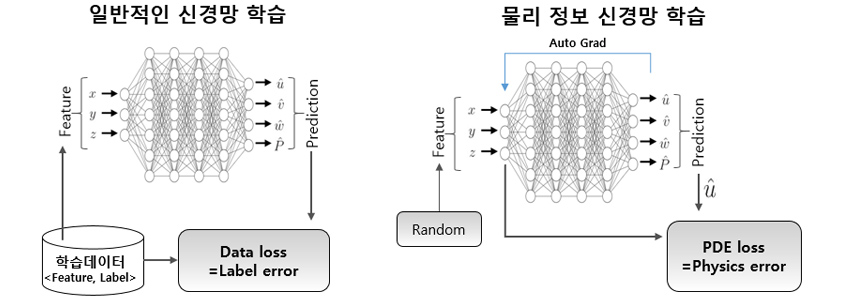
일반적인 신경망이 물리적 법칙을 고려하지 않고 데이터에 전적으로 의존하는 반면, 물리 정보 신경망은 지배방정식(물리방정식)을 만족하도록 식에 내제되어 있는 물리 정보를 신경망에 도입하는 방법입니다.

[그림 2] 일반적인 신경망과 물리 정보 신경망의 학습 방법

일반적인 신경망은 학습 데이터만을 사용하여 학습하며 손실 함수는 원본 데이터와 학습 모델에서 예측한 데이터에서의 레이블의 불일치 정도를 최소화하도록 학습하는 반면, 물리 정보 신경망은 물리 방정식 자체를 손실 함수에 사용하여 샘플링한 데이터가 물리 법칙을 만족하도록 학습을 진행합니다.

전통적인 시뮬레이션 방법은 도메인을 작은 요소로 나누어 각각에 대해서 계산합니다. 이 과정에서 도메인을 작은 요소로 나누는 Meshing 기법을 사용하지만 물리 정보 신경망을 사용하면 데이터를 단지 샘플링만 하기 때문에 도메인을 작은 요소로 나누는 등 추가적인 계산이 필요 없어지게 되는 장점이 있습니다. 실제 시뮬레이션은 학습(Train)을 진행한 후 추론(Inference)을 통하여 진행하게 됩니다. 이 과정에서 물리적인 법칙을 만족하는 신경망을 찾았기 때문에 물리 법칙을 만족하는 시뮬레이션이 가능하게 됩니다. 학습에 비해 추론하는 시간은 매우 작기 때문에 시뮬레이션하려는 도메인에 대해 한 번 학습을 진행하면 추론을 통한 반복 시뮬레이션을 매우 빠른 시간에 할 수 있다는 장점이 있습니다.

이러한 장점에도 불구하고 현재 물리 정보 신경망은 학습의 수렴성 문제, 전통적인 시뮬레이션 방법에 비하면 아직은 높지 않은 정확도 등의 단점이 존재하여 최근에는 전통적인 시뮬레이션 방법과 물리 정보 신경망을 이용한 방법을 합친 하이브리드 시뮬레이션에 대한 연구가 시작되고 있습니다.

하이브리드 시뮬레이션

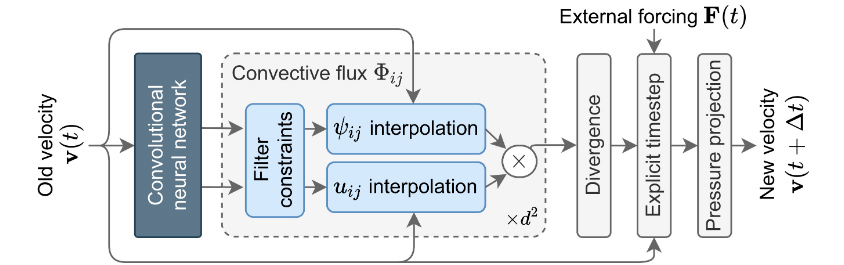
하이브리드 시뮬레이션이란 전통적인 시뮬레이션과 물리 정보 신경망을 이용한 시뮬레이션을 혼합한 방법입니다. 혼합하는 방법에 따라 크게 두 가지 방법이 존재하며 먼저 전통적인 시뮬레이션 방법에 계산시간이 큰 부분을 신경망으로 대체하는 방법에 대해 살펴보겠습니다.

[그림 3] 시간이 많이 걸리는 계산을 물리 정보 신경망으로 대체^[1]

전통적인 방법이 물리 정보 신경망에 비해 정확도가 높기 때문에 전체적인 프레임워크는 전통적인 수치해석 방법으로 진행하나 시간이 많이 걸리는 계산을 신경망으로 대체하였습니다. 유체해석을 위한 Navier-Stokes 방정식을 푸는 것으로, 단일 Time Step에 대한 흐름도를 보여준 것으로 Convective Flow 계산 시 기존 Standard Numerical Solver를 Convolutional Neural Network을 사용하여 대체하였습니다. 이렇게 하였을 때 전통적인 방법에 비해 상당한 정도의 속도 향상을 이루었다고 합니다.

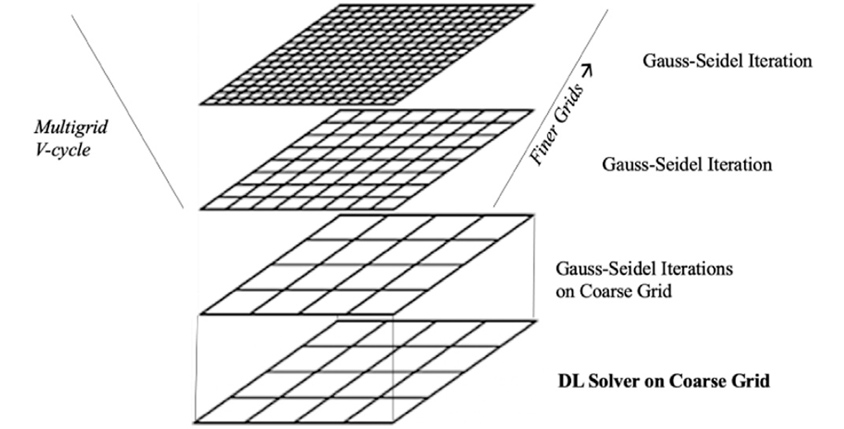
다른 한 가지 방법으로는 물리 정보 신경망의 빠른 시뮬레이션 속도를 이용하여 근사치까지 신경망으로 계산한 후 더 정확한 계산을 위해 전통적인 수치해석 방법을 사용하는 것입니다.

[그림 4] 물리 정보 신경망으로 계산 시간을 줄인 후 전통적인 방법으로 정확도를 보정^[2]

도메인의 Mesh를 크게 하여 물리 정보 신경망(Deep Learning Solver 사용)으로 시뮬레이션하여 대략적인 값을 얻은 후 더 정확한 계산을 위해 Gauss-Seidel(Standard Solver)을 사용하는 방법으로 전통적인 수치해석 기반 시뮬레이션에 비해 큰 속도 향상을 얻을 수 있습니다.

결론

최근 화두가 되고 있는 AI 기법을 도입한 물리 정보 신경망에 대해 알아보았습니다. AI의 발전에 따라 시뮬레이션 분야에서도 AI가 도입됨은 어찌 보면 당연한 처사입니다. 또한 AI를 구동할 수 있는 GPU와 같은 가속기의 발전에 따라 물리 정보 신경망은 계속해서 발전할 것으로 예상되며 빠른 시뮬레이션 속도로 인한 실시간 시뮬레이션이 가능하기 때문에 Digital Twin 등 응용 분야가 많은 것이 예상됩니다.

References
[1] Machine learning–accelerated computational fluid dynamics, D Kochkova, JA Smitha, A Alieva, Q Wanga, MP Brenner, and S Hoyera, Proceedings of the National Academy of Sciences, 2021
[2] The Old and the New: Can Physics-Informed Deep-Learning Replace Traditional Linear Solvers?, S Markidis, Frontiers in Big Data, 2021

▶ 해당 콘텐츠는 저작권법에 의하여 보호받는 저작물로 기고자에게 저작권이 있습니다.
▶ 해당 콘텐츠는 사전 동의 없이 2차 가공 및 영리적인 이용을 금하고 있습니다.

이 글이 좋으셨다면 구독&좋아요

여러분의 “구독”과 “좋아요”는
저자에게 큰 힘이 됩니다.

문기효 인공지능/애널리틱스 전문가

삼성SDS 고성능컴퓨팅연구Lab

슈퍼컴퓨터를 이용한 수치해석 분야를 연구하여 박사학위를 취득하였습니다. LLM 추론 및 HPC 시뮬레이션 가속을 연구하고 있으며 양자 컴퓨팅 등 미래 컴퓨팅 기술에 관심이 많습니다.