
New Hadoop3 Release
더그 커팅(Doug Cutting)이 하둡(Hadoop)을 최초로 선보인 지 벌써 12년이라는 시간이 흘렀습니다. 하둡의 성장과정을 보면 오픈소스의 집단지성과 잘 만든 플랫폼의 확장성이 얼마나 대단한지 실감할 수 있습니다. 하둡이 처음 나왔을 때는 많은 사람들이 하둡을 단순히 빅데이터를 처리할 수 있는 솔루션으로 생각했습니다. 하둡이 HDFS와 MapReduce를 기반으로 한 데이터 분산처리 소프트웨어였기 때문이죠. 시대적인 영향도 있었겠지만 사람들은 기존에 처리할 수 없던 데이터를 처리함으로써 새로운 인사이트가 나올 것을 기대했고, 이러한 작업들을 쉽게 하기 위해서 Solr, Pig, Zookeeper, HBase, Hive와 같은 초창기 파생 프로젝트들이 생겨났습니다. 또, 프로젝트 간의 협력이 중요해지면서 이들이 공통적으로 연계된 하둡의 인터페이스가 자연스럽게 플랫폼화됐습니다. 대표적인 인터페이스인 FileSystem(HDFS), Input/Output format(MapReduce)과 같은 소스는 이미 수많은 곳에서 확장되어, 이쪽 분야에서는 반드시 구현해야 하는 필수 스펙 중 하나라고 해도 과언이 아닙니다.
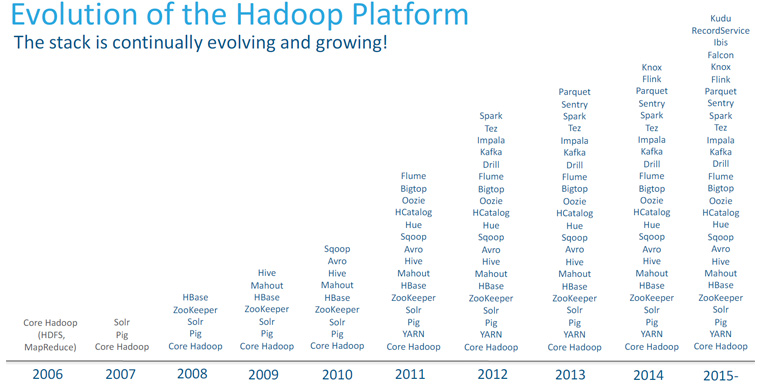 [그림1] 2006년 Hadoop의 시작부터 현재까지 에코시스템의 발전 (출처: Cloudera)
[그림1] 2006년 Hadoop의 시작부터 현재까지 에코시스템의 발전 (출처: Cloudera)
지금까지도 많이 사용하고 있는 하둡 2.x 버전은 2013년에 출시되었고, 그동안 수많은 마이너 버전업을 거쳐 2017년 12월에는 하둡 3.x 버전이 정식 출시되었습니다. (버그패치가 이뤄진 최신 버전은 2018년 4월 발표된 3.1.0 버전입니다.)
| # | Feature |
|---|---|
| 1 | HDFS Erasure Coding (HDFS-EC) |
| 2 | YARN Timeline Service v.2 |
| 3 | Shell Script Rewrite |
| 4 | MapReduce task-level native optimization |
| 5 | Support for Multiple Stanby NameNodes |
| 6 | Java 8 Minimum Runtime Version |
| 7 | New Default Ports for Several Services |
| 8 | Intra-DataNode Balancer |
| 9 | Reworked daemon and task heap management |
지금까지도 많이 사용하고 있는 하둡 2.x 버전은 2013년에 출시되었고, 그동안 수많은 마이너 버전업을 거쳐 2017년 12월에는 하둡 3.x 버전이 정식 출시되었습니다. (버그패치가 이뤄진 최신 버전은 2018년 4월 발표된 3.1.0 버전입니다.)
HDFS Erasure Coding
HDFS는 하나의 파일을 N개의 블록으로 분산 저장하는 파일시스템입니다. 이 HDFS의 주요 기능 중 하나가 Fault-tolerance인데, 하나의 파일을 이루고 있는 N개의 블록 중 몇 개가 유실되더라도 파일의 접근성을 보장하고 복구할 수 있는 기능입니다. 2.x 버전까지는 이 기능을 단순히 여러 개의 블록을 저장함으로써 구현했습니다. 블록이 하나 없어지더라도 복사해놓은 똑같은 블록 중 하나라도 살아있으면 복구가 가능한 것이죠. 이를 위해 일반적으로 각각 다른 디스크에 3개의 블록을 만들어 보관합니다. 이 기능은 매우 유용하지만 파일 1개를 저장하는 데 3배의 용량을 필요로 한다는 단점이 있습니다. 1GB 파일을 저장하려면 3GB가 필요한 셈이죠. 3.x 버전에서는 이를 RAID(Redundant Array of Inexpensive Disks)에서 주로 사용하는 Reed-Solomon 알고리즘을 사용한 ‘Erasure Coding’이라는 방법으로 개선하였습니다. Erasure Coding은 파일을 N개 블록으로 나누면서 N의 절반인 M개의 Parity 블록을 생성하여 Fault-tolerance를 보장하는 방식입니다.
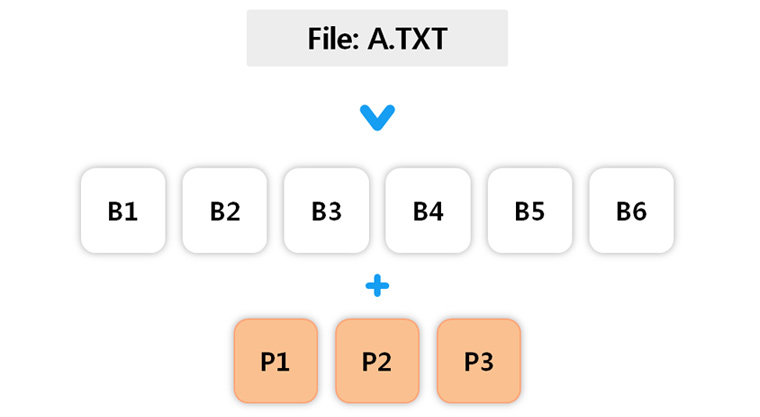 [그림2] 6개의 데이터블록과 3개의 Parity블록으로 나눠지는 (6, 3) Reed-Solomon
[그림2] 6개의 데이터블록과 3개의 Parity블록으로 나눠지는 (6, 3) Reed-Solomon
| N-replication | (N, M)Reed-solomon | |
|---|---|---|
| Fault-tolerance 보장 | N-1 | M |
| 1개 파일당 디스크 사용량 | 3N | 1.5N |
결론적으로 6, 3 Reed-solomon을 적용하면 디스크 용량을 50%나 절약할 수 있습니다. N-replication 방식의 경우 N-1개의 블록이 유실되더라도 파일을 읽을 수 있다면, Reed-solomon 방식은 최대 M개가 유실되더라도 파일을 읽을 수 있습니다. 더 자세히 알아보기 위해 아래와 같이 1부터 16까지의 숫자가 적혀있는 16byte 파일이 있다고 가정해보겠습니다.
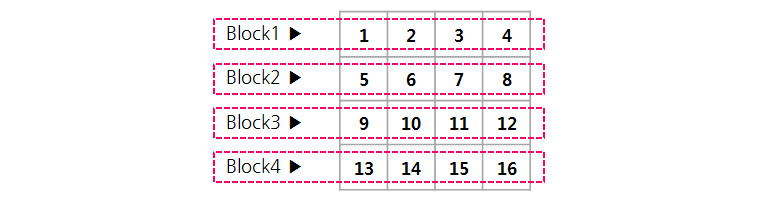
이 데이터는 블록이 4개이므로 N이 4이고, 따라서 M은 그 절반인 2입니다. 이 (4, 2) Reed-solomon 알고리즘은 데이터 블록들로부터 Parity블록들을 만들기 위해 x1~x8을 상수 값으로 하는 Encoding(Generator) matrix를 생성하여 새로운 블록을 계산합니다.
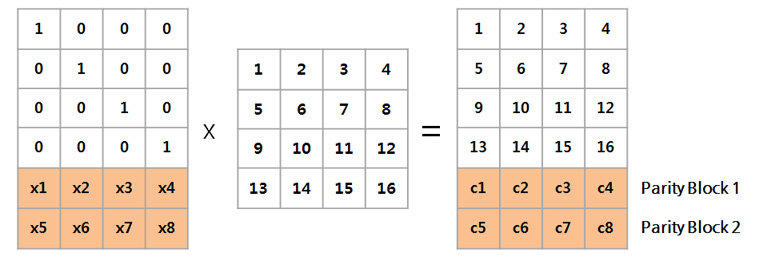
여기서 x1~x8의 경우 data의 크기와 블록의 개수에 따라 고정적이기 때문에 따로 저장할 필요 없이, 우측에 새로 생성된 Data+Parity블록이 실제로 디스크에 저장됩니다. 따라서 원래 4개였던 블록을 6개로 저장하였으므로 1.5N만큼의 디스크만 있으면 저장이 가능합니다. 또한 위의 [표2]에서 보듯 M개의 Fault-tolerance를 제공하므로 데이터 또는 Parity 블록이 M개 없어지더라도 원본 복구가 가능합니다. 만약 Block 3, 4가 유실되었다면, 다음과 같은 과정으로 복구할 수 있죠.
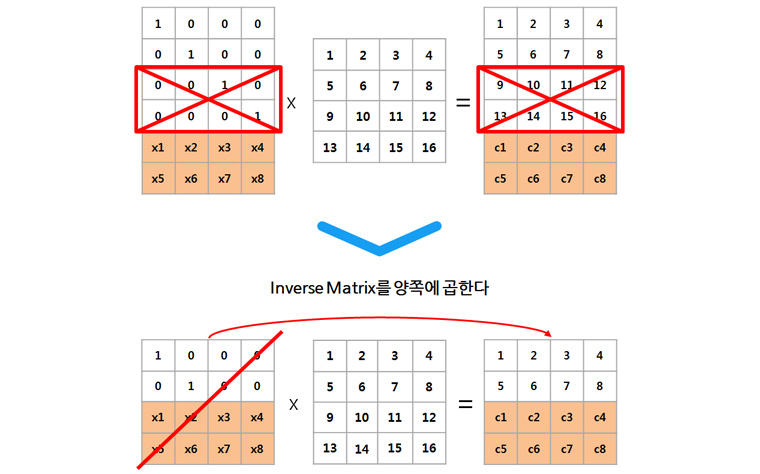
3, 4번 행이 삭제된 좌측 Encoding Matrix의 역행렬을 취하여 양쪽에 곱해주면, 우변이 유실된 데이터와 Encoding Matrix 역행렬의 곱이 되어 좌변의 원본 데이터를 계산할 수 있는 것입니다.
물론 이 알고리즘을 수행하려면 단순한 복사에 비해 인코딩/디코딩에 많은 CPU 연산이 들어가 성능이 저하될 수 있습니다. 하지만 이 문제는 Intel이 제공하는 ISA-L 코더 덕분에 어느 정도 해결되었습니다.
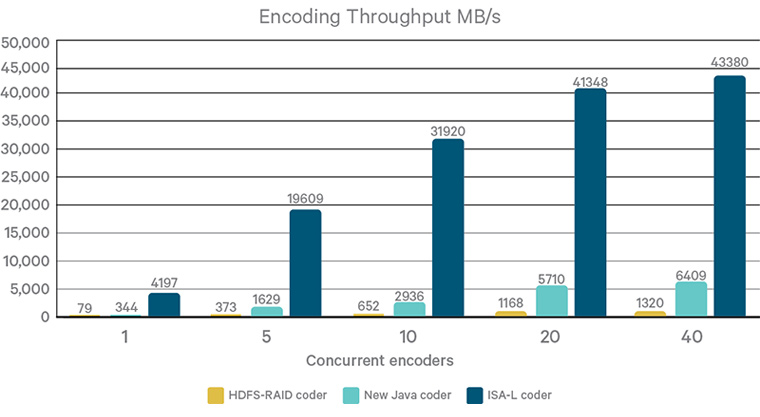
지금까지 Hadoop3의 신기능 중 하나인 Erasure Coding에 대하여 알아봤습니다. Hadoop3는 이 외에도 많은 기능들이 개선되었으니, 관련 업무나 공부를 하는 분들이라면 더 찾아 보시길 추천드립니다.
▶ 해당 콘텐츠는 저작권법에 의하여 보호받는 저작물로 기고자에 저작권이 있습니다.
▶ 해당 콘텐츠는 사전 동의없이 2차 가공 및 영리적인 이용을 금하고 있습니다.
![]()

삼성SDS 분석플랫폼Lab
삼성SDS 연구소 분석플랫폼Lab 소속이며, 소프트웨어 개발, 빅데이터 아키텍쳐, 머신러닝에 관한 지식과 업무 경험을 바탕으로 현재 삼성 SDS Brightics 솔루션 개발을 담당하고 있습니다.
